Before Google’s Social Graph API closed last month, I was able to gain access to a reasonable subset: 7,100,000 relationships across 1,500,000 sites (shown below). To be honest, it wasn’t what I was expecting.
The attach rate $latex \left(P\left(k\right) \sim{} k^{-\gamma}\right)$ is pretty close to what Barabasi, Albert, and Jeong found in Scale-free characteristics of random networks. $latex \gamma \sim{} 2.11$ across all, with $latex R^2 = 0.86$. $latex \gamma \sim{} 2.73$ for nodes with fewer than 101 attachments; $latex R^2 = 0.97$.
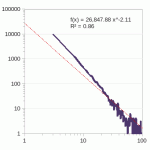
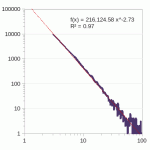
Even though that was not much different, what clearly stood out was the sizable amount of neighborhoods.
Following are compressed neighbor matrices for three random networks, and what was observed in the blog network. While each have standout patterns, the blogs is nothing like the others.




Leave a Reply
You must be logged in to post a comment.